1.2 二进制
1.2.1 问题02: 二进制加法
输入两个表示二进制的字符串,计算其和并以二进制字符串形式输出。
如,“11” 和 “01”,则输出“101”。
1.2.1.1 分析
若直接将字符串转换成数字类型,因为没有确定字符串的长度,所以会导致溢出。
可将字符按位对齐,以逢二进一的规则计算。
1.2.1.2 题解
package soint
import (
"unsafe"
)
func addBinary(a, b string) string {
lenA, lenB := len(a), len(b)
buf := make([]byte, max(lenA, lenB)+1)
carry := 0
// 从最低位开始
for i, j := lenA-1, lenB-1; i >= 0 || j >= 0; {
digitA, digitB := 0, 0
if i >= 0 {
digitA = toDigit(a[i])
}
if j >= 0 {
digitB = toDigit(b[j])
}
// 按位计算
digitSum := digitA + digitB + carry
var charSum byte = '0'
if digitSum > 1 {
carry = 1
if digitSum > 2 {
charSum = '1'
}
}
if digitSum == 1 {
charSum = '1'
carry = 0
}
if digitSum == 0 {
carry = 0
}
// 存入结果
buf[max(i, j)+1] = charSum
i--
j--
}
if carry > 0 {
buf[0] = '1'
} else {
buf = buf[1:] // 首位为0,则抛弃
}
// 将字节数组转化为字符串
result := unsafe.String(unsafe.SliceData(buf), len(buf))
return result
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func toDigit(c byte) int {
if c-'0' == 1 {
return 1
}
return 0
}
1.2.2 问题03:前n个数字二进制形式中1的个数
输入非负数n,计算0到n之间每个数字的二进制形式中1的个数,并输出一个数组。
如n为4, 对应数字为[0, 1, 2, 3, 4],二进制1的个数为[0, 1, 1, 2, 1],需输出数组[0, 1, 1, 2, 1]。
1.2.2.1 分析&题解
此问题可转化为计算一个非负数n其二进制形式中1的数量
根据 i&(i-1)计算 TC: O(nk)
对于二进制数i, i&(i-1)会将最右边的1转化为0。那么当所有的1为0时,计算次数即为1的数量。
k位二进制,1的最大个数为k,循环执行次数最大为k。整体时间复杂度为O(nk)。
func countBitsOnk(num int) []int {
result := make([]int, num+1)
for i := 0; i <= num; i++ {
result[i] = countBitsOkOfOneNum(i)
}
return result
}
func countBitsOkOfOneNum(num int) int {
count := 0
for i := num; i != 0; {
count++
i = i & (i - 1)
}
return count
}
根据 i 比 i&(i-1) 1的个数多1计算 TC: O(n)
由于数字i 比i&(i-1)的个数多一个1,那么可以利用之前已经计算过的结果来计算新结果。
此时计算一个数组的时间复杂度为O(1),整体时间复杂度为O(n)。
func countBitsOn(num int) []int {
result := make([]int, num+1)
for i := 1; i <= num; i++ {
result[i] = result[i&(i-1)] + 1
}
return result
}
根据i/2计算 TC:O(n)
因为奇数的二进制最低位一定是1,所以
- 若
i为偶数, 则i>>1和i的1的个数相同 - 若
i为奇数, 则i>>1比i的1的个数少一个
使用位运算代替四则运算,效率更高:
i>>1代替i/2i&1代替i%2
func countBitsOnWithBitOperation(num int) []int {
result := make([]int, num+1)
for i := 1; i <= num; i++ {
result[i] = result[i>>1] + (i & 1)
}
return result
}
Benchmark:
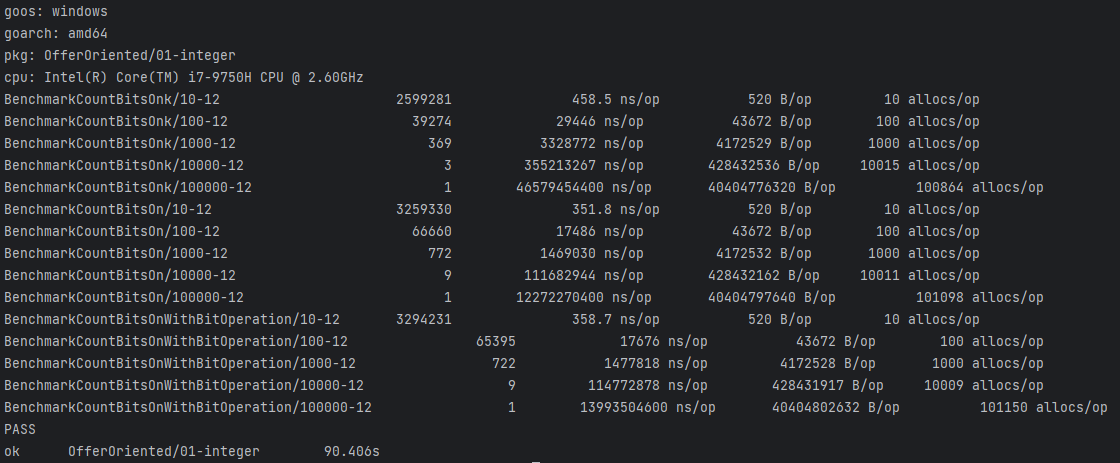
1.2.3 问题04: 只出现一次的数字
输入整数数组, 数组中只有一个数字出现了一次, 其他的都出现了三次. 请找出只出现一次的数字.
例: [0, 1, 0, 1, 0, 1, 100], 只出现一次的数字是100.
1.2.3.1 简化版: 其他的都出现了两次
如果其他的只出现了两次, 那么根据 一个数字和自身做异或运算,结果一定为0, 将所有的数字进行异或运算, 那么结果就是只出现一次的数字.
func singleNumberOther2Times(nums []int) int {
result := 0
for i := range nums {
result ^= nums[i]
}
return result
}
1.2.3.2 分析
若将每个数字当作二进制数来看, 那么将所有数字的相同位置的数相加, 若:
- 能够被 3 整除, 那么单独的数字此处一定是0
- 若被3除后余1, 那么单独的数字此处一定是1
func singleNumberOther3Times(nums []int64) int64 {
buf := make([]int64, 64)
for i := 0; i < len(nums); i++ {
for j := 0; j < 64; j++ {
buf[j] += (nums[i] >> (63 - j)) & 1
}
}
var result int64
for i := 0; i < 64; i++ {
u := buf[i] % 3
result = (result << 1) + u
}
return result
}
1.2.4 进阶: 只有一个数字出现m次, 其余都是n次,且m不能被n整除
思路和三次相同, 出现n次的位置一定能被n整除, 若被n整除余1那么一定是出现了m次的数字.
实际上计算结果只和其他数字出现次数有关
func mTimesNumberOtherNTimes(nums []int64, n int64) int64 {
buf := make([]int64, 64)
for i := 0; i < len(nums); i++ {
for j := 0; j < 64; j++ {
buf[j] += (nums[i] >> (63 - j)) & 1
}
}
var result int64
for i := 0; i < 64; i++ {
if buf[i]%n != 0 {
result = (result << 1) + 1
} else {
result = result << 1
}
}
return result
}
1.2.4 问题05: 单词长度的最大乘积
输入字符串数组 words, 计算不包含相同字符的字符串word[i]和word[j]的长度乘积的最大值. 若每个都至少包含一个相同字符则输出0.假设仅包含小写字母
例: [“ab”, “bd”, “ef”, “pq”, “qwe”, “asd” ], 其中长度乘积有 4, 9, 输出9
1.2.4.1 分析&题解
暴力解法 TC: O()
扫描每个字符串的字符并进行比较, 假设长度分别为 p, q, 那么单元操作时间复杂度为 O(pq), 当数组长度为n时, 整体时间复杂度将为,即
func bruteForce(strs []string) int {
product := 0
for i := 0; i < len(strs); i++ {
for j := i + 1; j < len(strs); j++ {
if compareStr(strs[i], strs[j]) {
p := len(strs[i]) * len(strs[j])
if product < p {
product = p
}
}
}
}
return product
}
func compareStr(a, b string) bool {
for i := 0; i < len(a); i++ {
for j := 0; j < len(b); j++ {
if a[i] == b[j] {
return false
}
}
}
return true
}
哈希表
使用哈希表来优化时间效率, 因为只包含26个小写字母, 所以可以创建长度为26的布尔型数组来模拟哈希表:
- 为每个字符串, 创建哈希表, 存储26个字母的出现情况
- 两两比较字符串, 查询哈希表中是否出现了同一字母
哈希表的查找时间复杂度为O(1), 比较哈希表中的字母(长度固定为26), 所以时间复杂度为O(1).
创建哈希表时, 字符串数组长度为n, 字符串长度为k, 那么创建哈希表的时间复杂度为O(nk).
字符串两两比较时的时间复杂度为O()
那么总体的时间复杂度为O() or O() .
创建哈希表的空间复杂度为O(n).
func Test_maxProductHashTable(t *testing.T) {
type args struct {
strs []string
}
tests := []struct {
name string
args args
want int
}{
// TODO: Add test cases.
{name: "empty string array", args: args{strs: []string{}}, want: 0},
{name: "contains empty element", args: args{strs: []string{"ab", "", "ef", "", "qwe", "asd"}}, want: 9},
{name: "01", args: args{strs: []string{"ab", "bd", "ef", "pq", "qwe", "asd"}}, want: 9},
{name: "02", args: args{strs: []string{"asb", "bsd", "dse", "esf", "fsg", "gsh"}}, want: 0},
}
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
if got := maxProductHashTable(tt.args.strs); got != tt.want {
t.Errorf("maxProductHashTable() = %v, want %v", got, tt.want)
}
})
}
}
整数二进制数位
由于字符串中出现字符只会有两种情况: true, false. 所以可以使用二进制的 0, 1来表示.
出现的字符共有26个, 那么可以使用32位整数来存储.
比较字符串时, 只要将代表的两个整数进行与运算, 只要不为0, 那么一定表示有相同的字母
总体的时间复杂度为O() or O() .
创建哈希表的空间复杂度为O(n).
但因为使用位运算, 效率比逻辑运算要高.
func maxProductBinary(strs []string) int {
// create binary slice
b := make([]int32, len(strs))
for i := 0; i < len(strs); i++ {
for _, c := range strs[i] {
b[i] |= 1 << (c - 'a')
}
}
// compare strings
result := 0
for i := 0; i < len(strs); i++ {
for j := i + 1; j < len(strs); j++ {
if b[i]&b[j] == 0 {
p := len(strs[i]) * len(strs[j])
if result < p {
result = p
}
}
}
}
return result
}
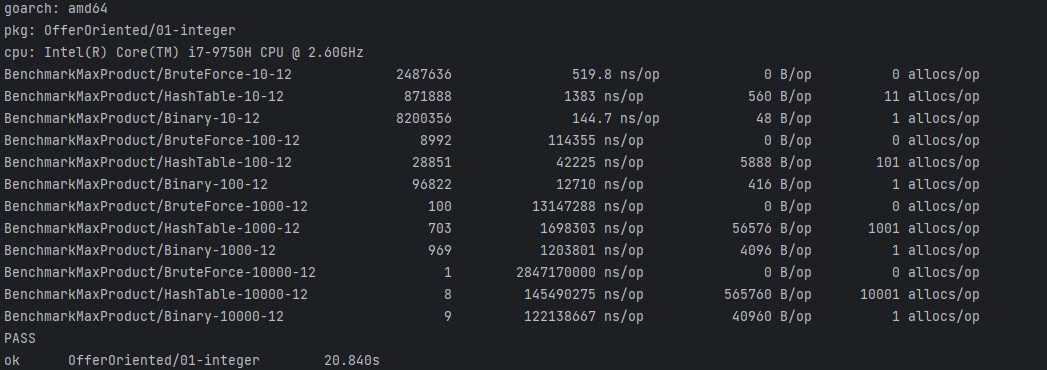
Benchmark