8.3 二叉搜索树
二叉搜索树是一种特殊二叉树:
- 左子节点 < 根节点
- 右子节点 > 根节点
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree.
针对二叉搜索树, 通常使用中序遍历, 其遍历结果将是有序的.
由于二叉搜索树的特性, 在查找元素时, 只需查找某一边子树(大于则为右子树, 小于则为左子树). 其时间复杂度为 O(h) (h为二叉搜索树的高度)
二叉搜索树的查找:
func searchBST(root *TreeNode, val int) *TreeNode {
cur := root
for cur != nil {
if val == cur.Val {
break
}
// 左子树
if val < cur.Val {
cur = cur.Left
}
// 右子树
if val > cur.Val {
cur = cur.Right
}
}
return cur
}
8.3.1 问题52: 展平二叉搜索树
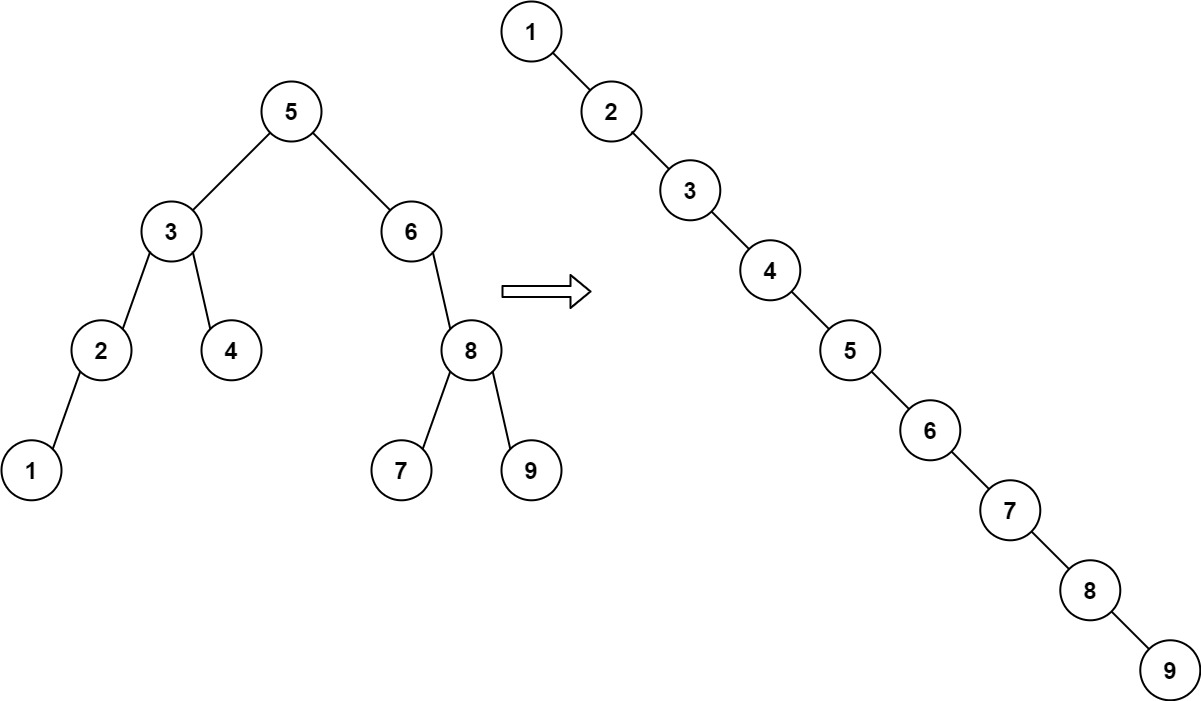
给你一棵二叉搜索树,请 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:
img 输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9] 输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]示例 2:
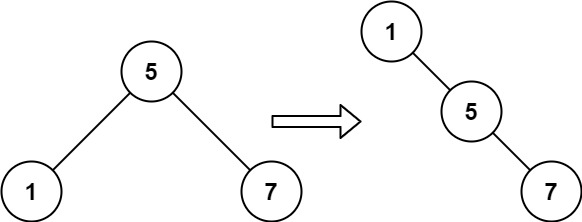
img 输入:root = [5,1,7] 输出:[1,null,5,null,7]提示:
- 树中节点数的取值范围是
[1, 100]0 <= Node.val <= 1000
8.3.1.1 分析&题解
二叉搜索树的最底层的最左节点一定是最小节点, 那么这个节点一定是展开后的根节点.
因为要断开左节点, 然后连接至根节点的右节点; 顺序为左中右, 所以使用中序遍历.
func increasingBST(root *TreeNode) *TreeNode {
st := make([]*TreeNode, 0) // stack
cur := root // current node
var prev *TreeNode // previous node
var newRoot *TreeNode // new tree root
// inorder dsf
for cur != nil || len(st) > 0 {
// left
for cur != nil {
st = append(st, cur)
cur = cur.Left
}
// mid
cur = st[len(st)-1]
st = st[:len(st)-1]
// 连接到前一节点
if prev != nil {
prev.Right = cur
} else {
// 新树的根节点
newRoot = cur
}
// right
prev = cur
// 断开左子树
cur.Left = nil
cur = cur.Right
}
return newRoot
}
8.3.2 问题53: 二叉搜索树的下一个节点
给定一棵二叉搜索树和其中的一个节点
p,找到该节点在树中的中序后继。如果节点没有中序后继,请返回null。节点
p的后继是值比p.val大的节点中键值最小的节点,即按中序遍历的顺序节点p的下一个节点。示例 1:
img 输入:root = [2,1,3], p = 1 输出:2 解释:这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。示例 2:
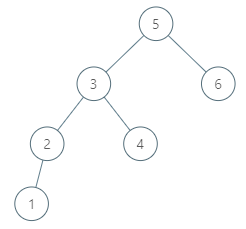
img 输入:root = [5,3,6,2,4,null,null,1], p = 6 输出:null 解释:因为给出的节点没有中序后继,所以答案就返回 null 了。提示:
- 树中节点的数目在范围
[1, 10^4]内。-10^5 <= Node.val <= 10^5- 树中各节点的值均保证唯一。
8.3.2.1 分析&题解
中序遍历二叉搜索树的结果一定是递增序列, 那么p的中序后继一定是大于p的节点中的最小的那个.
流程:
- 遍历, 比较当前节点
cur和pp > cur, 则进入右子树查找p < cur, 记录当前节点, 进入左子树查找
- 最后一个记录的节点就是
p的中序后继
时间复杂度: O(h), h为二叉搜索树的高度
func inorderSuccessor(root *TreeNode, p *TreeNode) *TreeNode {
var res *TreeNode
cur := root // current node
for cur != nil {
if cur.Val > p.Val {
// left tree
// record result
res = cur
cur = cur.Left
} else {
// right tree
cur = cur.Right
}
}
return res
}
8.3.3 问题54: 所有大于等于节点的值之和
定一个二叉搜索树,请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
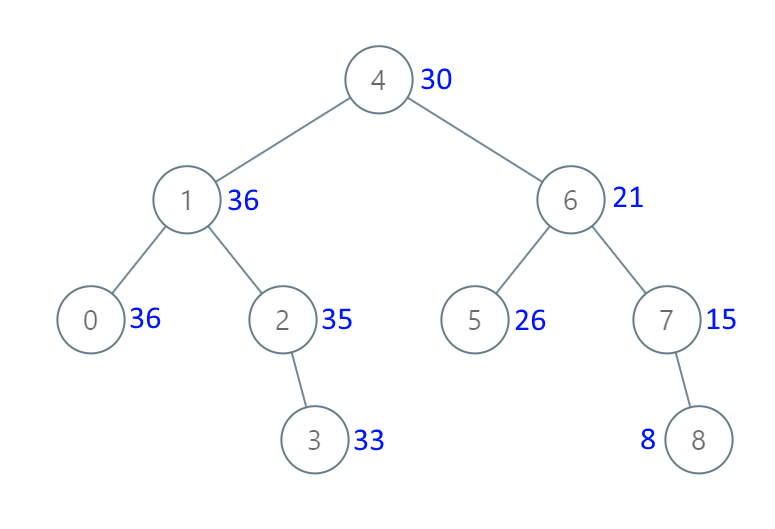
输入:root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]示例 2:
输入:root = [0,null,1] 输出:[1,null,1]示例 3:
输入:root = [1,0,2] 输出:[3,3,2]示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]提示:
- 树中的节点数介于
0和10^4之间。- 每个节点的值介于
-10^4和10^4之间。- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
8.3.3.1 分析&题解
若从大到小来遍历, 那么节点序列可看作 , (). 对节点, 比它大的节点已经遍历过, 那么此时 的新值就是之前的节点和.
中序遍历二叉搜索树, 结果是递增的; 将中序遍历的顺序颠倒, 先遍历右子树, 那么结果就是递减的.
func convertBST(root *TreeNode) *TreeNode {
st := make([]*TreeNode, 0) // stack
cur := root
sum := 0
for cur != nil || len(st) > 0 {
// right tree
for cur != nil {
st = append(st, cur)
cur = cur.Right
}
// sum
cur = st[len(st)-1]
st = st[:len(st)-1]
sum += cur.Val
cur.Val = sum
// left tree
cur = cur.Left
}
return root
}
8.3.4 问题55: 二叉搜索树迭代器
实现一个二叉搜索树迭代器类
BSTIterator,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点root会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext()如果向指针右侧遍历存在数字,则返回true;否则返回false。int next()将指针向右移动,然后返回指针处的数字。注意,指针初始化为一个不存在于 BST 中的数字,所以对
next()的首次调用将返回 BST 中的最小元素。可以假设
next()调用总是有效的,也就是说,当调用next()时,BST 的中序遍历中至少存在一个下一个数字。示例:
img 输入 inputs = ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"] inputs = [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []] 输出 [null, 3, 7, true, 9, true, 15, true, 20, false] 解释 BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); bSTIterator.next(); // 返回 3 bSTIterator.next(); // 返回 7 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 9 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 15 bSTIterator.hasNext(); // 返回 True bSTIterator.next(); // 返回 20 bSTIterator.hasNext(); // 返回 False提示:
- 树中节点的数目在范围
[1, 10^5]内0 <= Node.val <= 10^6- 最多调用
10^5次hasNext和next操作进阶:
- 你可以设计一个满足下述条件的解决方案吗?
next()和hasNext()操作均摊时间复杂度为O(1),并使用O(h)内存。其中h是树的高度。
8.3.4 分析&题解
根据二叉树的中序遍历的迭代代码可知, 遍历的条件就是是否存在下一节点, 即hasNext. 而获取下一节点的代码就是遍历循环的循环体.
SC: O(h), h为二叉树高度, 维护一个栈
TC: 平均为O(1), 调用n次next 遍历完二叉树
type BSTIterator struct {
cur *TreeNode // curren node
st []*TreeNode // stack
}
func Constructor(root *TreeNode) BSTIterator {
return BSTIterator{
cur: root,
st: make([]*TreeNode, 0),
}
}
func (bi *BSTIterator) Next() int {
// left tree
for bi.cur != nil {
bi.st = append(bi.st, bi.cur)
bi.cur = bi.cur.Left
}
bi.cur = bi.st[len(bi.st)-1]
bi.st = bi.st[:len(bi.st)-1]
val := bi.cur.Val
// right tree
bi.cur = bi.cur.Right
return val
}
func (bi *BSTIterator) HasNext() bool {
return bi.cur != nil || len(bi.st) > 0
}
8.3.5 问题56: 二叉搜索树两个节点的值之和
给定一个二叉搜索树的 根节点
root和一个整数k, 请判断该二叉搜索树中是否存在两个节点它们的值之和等于k。假设二叉搜索树中节点的值均唯一。示例 1:
输入: root = [8,6,10,5,7,9,11], k = 12 输出: true 解释: 节点 5 和节点 7 之和等于 12示例 2:
输入: root = [8,6,10,5,7,9,11], k = 22 输出: false 解释: 不存在两个节点值之和为 22 的节点提示:
- 二叉树的节点个数的范围是
[1, 10^4].-10^4 <= Node.val <= 10^4root为二叉搜索树-10^5 <= k <= 10^5
8.3.5.1 分析&题解
哈希表
中序遍历+哈希表
TC: O(n) SC: O(n)
func findTarget(root *TreeNode, k int) bool {
m := make(map[int]bool, 0)
st := make([]*TreeNode, 0)
cur := root
for cur != nil || len(st) > 0 {
// left
for cur != nil {
st = append(st, cur)
cur = cur.Left
}
// node
cur = st[len(st)-1]
st = st[:len(st)-1]
if v, ok := m[k-cur.Val]; ok {
return v
}
m[cur.Val] = true
// right
cur = cur.Right
}
return false
}
双指针
由于二叉搜索树是有序的, 那么个可以创建两个相反方向的迭代器, 相当于相反的双指针.
问题就转换成了有序数组的两数之和的双指针解法.
TC: O(n), SC: O(h), h为二叉树高度, 因为高度远小于节点数, 所以空间复杂度小于O(n)
// TODO: 2023-09-12