heap 包源码阅读

最近在练习leetcode题目时，需要用到堆，发现 Golang 标准库已经有heap包，在使用的同时也看看源码的写法。

1. 堆的定义

In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C.

2. 数据结构

堆通常使用完全二叉树来实现并且完全二叉树可以使用数组来表示，故堆可以使用数组来实现。

堆的类型通常有两种：

1. 最大堆：父节点的元素一定大于等于子节点
2. 最小堆：父节点的元素一定小于等于子节点

数组中节点的关系

在用数组表示的堆中，假设当前节点为$N_i$，i为数组索引，则有：

1. 父节点索引为：$\frac{i-1}{2}$
2. 左子节点索引为：$2i+1$
3. 右子节点索引为：$2i+2$

3. 接口

heap包中的函数都是以接口类型的变量作为参数，这样做的好处：

1. 调用方可以通过接口与具体实现分离，解除上下游的耦合
2. 上层的模块不再需要依赖下层的具体模块，只需要依赖一个约定好的接口
3. 无需关心函数的具体实现，只要实现了约定的接口即可

heap包只有一个结构heap.Interface：

type Interface interface {
	sort.Interface
	Push(x any) // add x as element Len()
	Pop() any   // remove and return element Len() - 1.
}

将其中的sort.Interface展开后可以得到：

type Interface interface {
	Len() int
	Less(i, j int) bool
	Swap(i, j int)
	Push(x any) 
	Pop() any
}

也就是说实现heap.Interface需要实现上述的5个方法，因为堆是由数组实现的，所以实现的方法是针对数组及其元素：

1. Len：返回数组的大小
2. Less：比较数组中元素的大小
3. Swap：交换数组中元素
4. Push：向数组中添加元素
5. Pop：返回并删除数组的最后一个元素

4. 函数

以最小堆为例进行分析。

4.1 up(h, j) and down(h, i0, n)

heap.up和heap.down是包中最核心的函数，也是堆的最基础的操作：

• up：上浮，表示当前节点和其父节点交换；发生在新增节点时(Push)，此时节点在二叉树的最低层，判断是否需要上浮。
• down：下沉，表示当前节点与其子节点交换；发生在删除栈顶节点(Pop)时，将堆中的最后一个节点放到堆顶，判断是否需要下沉。

down

时间复杂度：$O(logn)$，n 为数组长度（堆的大小）；当节点需要交换至二叉树底部时，交换次数为二叉树高度h

func down(h Interface, i0, n int) bool {
	i := i0
	for {
		j1 := 2*i + 1
		if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
			break
		}
		j := j1 // left child
		if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
			j = j2 // = 2*i + 2  // right child
		}
		if !h.Less(j, i) {
			break
		}
		h.Swap(i, j)
		i = j
	}
	return i > i0
}

流程如下：

1. 将传入的索引记为当前索引
2. 获取左节点索引，若左节点不存在（左节点索引大于数组长度 或 数值溢出），则跳转至 步骤 7）
3. 获取右节点索引，若右节点存在且元素值小于左节点，则选择右节点
4. 比较当前节点，若不小于右节点，则跳转至 步骤 7）；
5. 交换当前当前节点和子节点（左右节点中较小的一个）
6. 更新当前节点索引，继续 步骤 1）
7. 返回当前节点索引是否大于传入索引

总体流程：

1. 将当前节点和最小的子节点交换，直到无法交换为止
2. 返回是否发生了下沉（节点交换）

up

时间复杂度：$O(logn)$，n 为数组长度（堆的大小）；当节点需要交换至二叉树顶部时，交换次数为二叉树高度h

func up(h Interface, j int) {
	for {
		i := (j - 1) / 2 // parent
		if i == j || !h.Less(j, i) {
			break
		}
		h.Swap(i, j)
		j = i
	}
}

流程：

1. 计算父节点的索引
2. 当前已经是堆顶 或 不小于父节点，跳转至步骤 5)
3. 交换当前节点和父节点
4. 更新当前节点，继续 步骤1）
5. 结束

总体流程：

1. 和父节点交换，直到堆顶 或者 不满足交换条件

4.2 Init(h)

初始化堆，当定义的数组存在初始元素是可以调用函数Init将其堆化(heapify)，即转化成堆。

func Init(h Interface) {
	// heapify
	n := h.Len()
	for i := n/2 - 1; i >= 0; i-- {
		down(h, i, n)
	}
}

此算法的时间复杂为$O(n)$。

为什么时间复杂度是 O(n)

详细证明可以参见How can building a heap be O(n) time complexity?。

假设树的高度$h=logn$，那么构建堆的交换次数计算如下：

$sum=0\times \frac{n}{2}+(1\times \frac{n}{4})+(2\times \frac{n}{8}+...+(h*1))$

证明过程：

Taylor series for buildHeap complexity

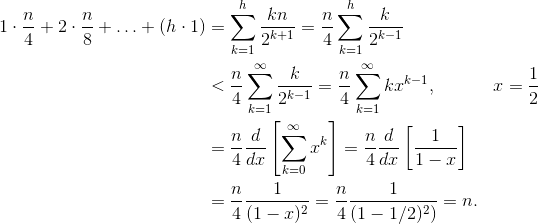
4.3 Pop and Push

时间复杂度均为 O(logn)

func Push(h Interface, x any) {
	h.Push(x)
	up(h, h.Len()-1)
}

func Pop(h Interface) any {
	n := h.Len() - 1
	h.Swap(0, n)
	down(h, 0, n)
	return h.Pop()
}

4.4 Remove

删除指定位置的元素，时间复杂度：O(logn)

func Remove(h Interface, i int) any {
	n := h.Len() - 1
	if n != i {
		h.Swap(i, n)
		if !down(h, i, n) {
			up(h, i)
		}
	}
	return h.Pop()
}

总体流程：

1. 将想要删除的元素和最后一个元素交换
2. 对最后一个元素进行上浮/下沉操作
3. 删除最后一个元素（值为想要删除的元素）

4.5 Fix

当元素的值（或者说优先级）被修改，调整其在堆中的位置，时间复杂度：O(logn)

func Fix(h Interface, i int) {
	if !down(h, i, h.Len()) {
		up(h, i)
	}
}

Reference

1. https://en.wikipedia.org/wiki/Heap_(data_structure)
2. https://github.com/golang/go/blob/release-branch.go1.20/src/container/heap/heap.go
3. https://stackoverflow.com/a/18742428/14963922