15.2 图的搜索

图的搜索分为:

• 广度优先搜索 使用先进先出的队列:

  1. 添加起始节点
  2. 节点出队, 将其相邻并且未访问过的节点入队, 重复 2) 直到队列为空

• 深度优先搜索

  • 使用后进先出的栈:

    1. 添加起始节点

    2. 节点出栈, 将其相邻且未访问过的节点入栈, 重复2) 直到栈为空

  • 递归: 沿着图的边尽可能的深入搜索, 直到没有相邻节点为止

若需要找出无权图中的节点间的最短距离, 建议使用广度优先算法.

若需要找出符合条件的路径, 则使用深度优先.

15.2.1 问题105: 最大面积岛屿

LCR 105. 岛屿的最大面积

给定一个由 0 和 1 组成的非空二维数组 grid ，用来表示海洋岛屿地图。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1:

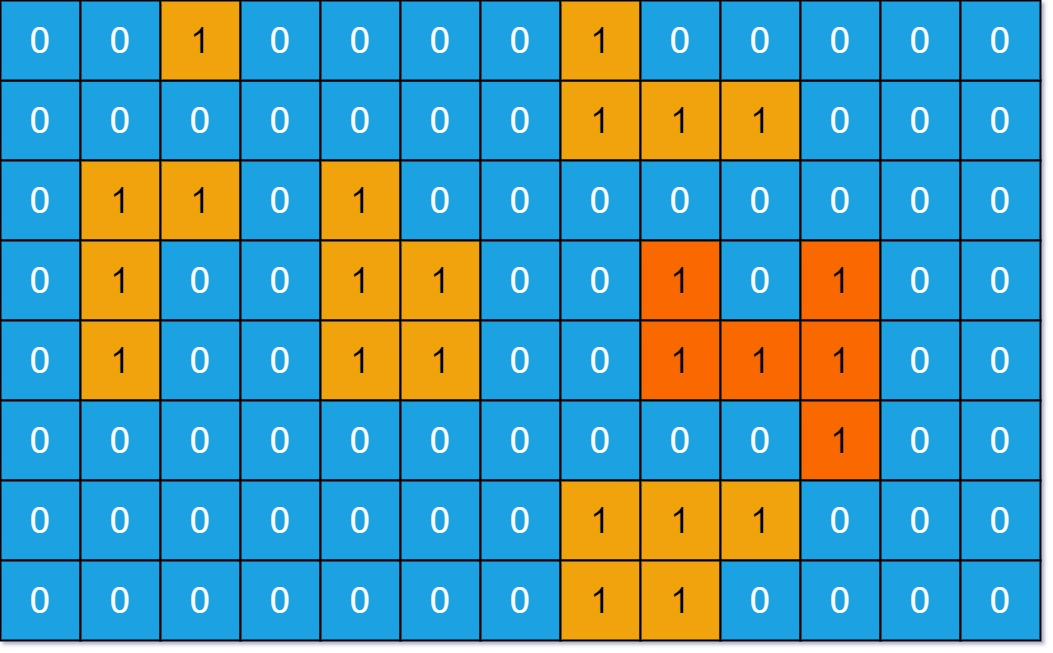
img

输入: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出: 6
解释: 对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

输入: grid = [[0,0,0,0,0,0,0,0]]
输出: 0

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] is either 0 or 1

15.2.1.1 分析&题解

将岛屿看作节点, 相邻的岛屿看作边相连. 那么整个矩阵就可以看作图, 相连的岛屿视作互不相连的子图, 子图内部的节点都是相连的.

此时岛屿面积就变成了图内节点的数目:

1. 扫描矩阵
2. 若遇到没有访问过的节点, 搜素此节点所在图的节点数, 计算面积.
3. 扫描完所有的节点, 得出最大的面积

func maxAreaOfIsland(grid [][]int) int {
    row, col := len(grid), len(grid[0])
    // 标识节点是否访问过
    visited := make([][]bool, row)
    for i := range visited {
        visited[i] = make([]bool, col)
    }
    
    maxArea := 0 // 最大面积
    // 扫描矩阵
    for r := range grid {
        for c := range grid[r] {
            // 找到岛屿节点 且 未访问过
            if grid[r][c] == 1 && !visited[r][c] {
                // 获取节点所在岛屿的面积
                area := getArea(grid, visited, r, c)
            	// 更新最大面积
                maxArea = max(maxArea, area)
            }
        }
    }
}

获取岛屿节点所在岛屿的最大面积, 即求节点所在图的所有节点数, 需要搜索图的所有节点, 有两种方式:

• 广度优先搜索
• 深度优先搜索

SC: O(mn), TC: O(mn)

若可以修改原矩阵数据, 那么在访问节点后将其值改为0, 无需辅助矩阵, SC 将降为 O(1)

广度优先搜索

要判断节点是否存在相邻的岛屿节点, 需要判断当前节点的上, 下, 左, 右四个方向是否有岛屿节点. 可以使用数组dirs{{-1, 0}, {1,0}, {0,-1}, {0,1}}表示四个方向, 移动坐标后即可到达四个方向的相邻节点.

广度优先搜索, 使用队列:

1. 将当前岛屿节点入队
2. 节点出队, 标识为已访问, 将其相邻节点入队, 计算节点数量.
3. 重复 2) 直到队列为空

func maxAreaOfIsland(grid [][]int) int {
    // 访问标记
    visited := make([][]bool, len(grid))
    for i := range visited {
        visited[i] = make([]bool, len(grid[0]))
    }

    maxArea := 0
    // 扫描矩阵
    for r := range grid {
        for c := range grid[r] {
            // 岛屿节点 && 未访问
            if grid[r][c] == 1 && !visited[r][c] {
                area := getAreaBFS(grid, visited, r, c)
                maxArea = max(maxArea, area)
            }
        }
    }

    return maxArea
}

func getAreaBFS(grid [][]int, visited [][]bool, i, j int) int {
    // Queue
    queue := make([][]int, 0)
    // 初始节点入队
    queue = append(queue, []int{i, j})
    visited[i][j] = true

    // 移动方向, 上下左右
    dirs := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
    area := 0
    row, col := len(grid), len(grid[0]) 
    // BFS, 搜索节点
    for len(queue) > 0 {
        // 当前节点出队
        cur := queue[0]
        queue = queue[1:]
        area++ 

        // 相邻节点入队
        for _, dir := range dirs {
            r := cur[0] + dir[0]
            c := cur[1] + dir[1]
            isValid := r >= 0 && r < row && c >= 0 && c < col
            // 合法坐标 && 岛屿节点 && 未访问
            if isValid && grid[r][c] == 1 && !visited[r][c] {
                // 入队
                queue = append(queue, []int{r, c})
                // 标记访问
                visited[r][c] = true
            } 
        }
    }

    return area
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

深度优先搜索 栈

要判断节点是否存在相邻的岛屿节点, 需要判断当前节点的上, 下, 左, 右四个方向是否有岛屿节点. 可以使用数组dirs{{-1, 0}, {1,0}, {0,-1}, {0,1}}表示四个方向, 移动坐标后即可到达四个方向的相邻节点.

深度优先搜索, 使用栈:

1. 将当前岛屿节点入栈
2. 节点出栈, 标识为已访问, 将其相邻节点入栈, 计算节点数量.
3. 重复 2) 直到队列为空

func maxAreaOfIsland(grid [][]int) int {
    // 访问标记
    visited := make([][]bool, len(grid))
    for i := range visited {
        visited[i] = make([]bool, len(grid[0]))
    }

    maxArea := 0
    // 扫描矩阵
    for r := range grid {
        for c := range grid[r] {
            // 岛屿节点 && 未访问
            if grid[r][c] == 1 && !visited[r][c] {
                area := getAreaDFS(grid, visited, r, c)
                maxArea = max(maxArea, area)
            }
        }
    }

    return maxArea
}

func getAreaDFS(grid [][]int, visited [][]bool, i, j int) int {
    // Queue
    st := make([][]int, 0)
    // 初始节点入栈
    st = append(st, []int{i, j})
    visited[i][j] = true

    // 移动方向, 上下左右
    dirs := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
    area := 0
    row, col := len(grid), len(grid[0]) 
    // DFS, 搜索节点
    for len(st) > 0 {
        // 当前节点出队
        cur := st[len(st)-1]
        st = st[:len(st)-1]
        area++ 

        // 相邻节点入队
        for _, dir := range dirs {
            r := cur[0] + dir[0]
            c := cur[1] + dir[1]
            isValid := r >= 0 && r < row && c >= 0 && c < col
            // 合法坐标 && 岛屿节点 && 未访问
            if isValid && grid[r][c] == 1 && !visited[r][c] {
                // 入队
                st = append(st, []int{r, c})
                // 标记访问
                visited[r][c] = true
            } 
        }
    }

    return area
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

深度优先搜索 递归

深度优先可以使用递归形式

func maxAreaOfIsland(grid [][]int) int {
    // 访问标记
    visited := make([][]bool, len(grid))
    for i := range visited {
        visited[i] = make([]bool, len(grid[0]))
    }

    maxArea := 0
    // 扫描矩阵
    for r := range grid {
        for c := range grid[r] {
            // 岛屿节点 && 未访问
            if grid[r][c] == 1 && !visited[r][c] {
                area := getAreaDFSRecursive(grid, visited, r, c)
                maxArea = max(maxArea, area)
            }
        }
    }

    return maxArea
}

func getAreaDFSRecursive(grid [][]int, visited [][]bool, i, j int) int {
    area := 1
    visited[i][j] = true
    dirs := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
    
    for _, dir := range dirs {
        r := i + dir[0]
        c := j + dir[1]
        isValid := r >=0 && r < len(grid) && c >=0 && c < len(grid[0])
        if isValid && grid[r][c] == 1 && !visited[r][c] {
            area += getAreaDFSRecursive(grid, visited, r, c)
        }
    }

    return area
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

15.2.2 问题106: 二分图

LCR 106. 判断二分图

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。

给定一个二维数组 graph ，表示图，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u] 不包含 u）。
• 不存在平行边（graph[u] 不包含重复值）。
• 如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例 1：

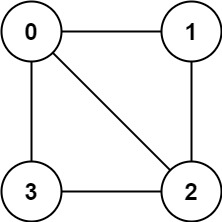
img

输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例 2：

img

输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。

提示：

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] 不会包含 u
• graph[u] 的所有值 互不相同
• 如果 graph[u] 包含 v，那么 graph[v] 也会包含 u

15.2.2.1 分析&题解

二分图可以将节点分为两种不同的类型, 那么可以将节点进行上色(标记), 如果所有的相邻节点颜色不同那么, 就是二分图; 如果有一个节点的和其相邻节点颜色相同, 则不是.

func isBipartite(graph [][]int) bool {
    // 着色标记
    colors := make([]int, len(graph))
    for i := range colors {
        colors[i] = -1
    }

    for i := range graph {
        if colors[i] == -1 {
            if !setColor(graph, colors, i, 0) {
                return false
            }
        }
    }

    return true
}

搜索节点可以使用: BFS 或者 DFS

广度优先

func isBipartite(graph [][]int) bool {
    // 着色标记
    colors := make([]int, len(graph))
    for i := range colors {
        colors[i] = -1
    }

    for i := range graph {
        if colors[i] == -1 {
            if !setColorBFS(graph, colors, i, 0) {
                return false
            }
        }
    }

    return true
}

func setColorBFS(graph [][]int, colors []int, i, c int) bool {
    // Queue
    queue := make([]int, 0)
    // 初始节点入队
    queue = append(queue, i)
    // 标记
    colors[i] = c
    
    // BFS
    for len(queue) > 0 {
        // 出队
        cur := queue[0]
        queue = queue[1:]

        // 相邻节点入队
        for _, adj := range graph[cur] {
            // 已着色但颜色相同, 不是二分图
            if colors[adj] != -1 {
                if colors[adj] == colors[cur] {
                    return false
                }
            } else { // 未着色
                // 入队
                queue = append(queue, adj)
                // 添加不同色
                colors[adj] = 1 - colors[cur]
            }
        }
    }

    return true
}

深度优先

func isBipartite(graph [][]int) bool {
    // 着色标记
    colors := make([]int, len(graph))
    for i := range colors {
        colors[i] = -1
    }

    for i := range graph {
        if colors[i] == -1 {
            if !setColorDFS(graph, colors, i, 0) {
                return false
            }
        }
    }

    return true
}

func setColorDFS(graph [][]int, colors []int, i, c int) bool {
    // Queue
    st := make([]int, 0)
    // 初始节点入队
    st = append(st, i)
    // 标记
    colors[i] = c
    
    // BFS
    for len(st) > 0 {
        // 出栈
        l := len(st)
        cur := st[l-1]
        st = st[:l-1]

        // 相邻节点入栈
        for _, adj := range graph[cur] {
            // 已着色但颜色相同, 不是二分图
            if colors[adj] != -1 {
                if colors[adj] == colors[cur] {
                    return false
                }
            } else { // 未着色
                // 入栈
                st = append(st, adj)
                // 添加不同色
                colors[adj] = 1 - colors[cur]
            }
        }
    }

    return true
}

15.2.3 问题107: 矩阵中的距离

LCR 107. 01 矩阵

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

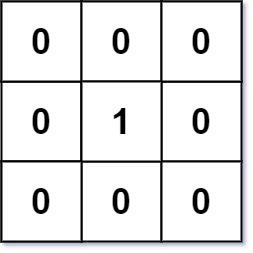
img

输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

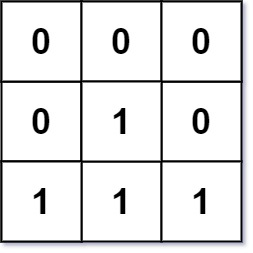
img

输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10^4
• 1 <= m * n <= 10^4
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0

15.2.3.1 分析&题解

将矩阵值看作节点, 相邻的位置的数字有边相连, 整个矩阵可以看作是图.

因为广度优先搜索能够保证起始节点到任意节点一定是最短路径, 那么将值为 0 的所有节点当作初始节点, 广度优先遍历子图, 即可找出所有节点到最近0的距离.

要避免重复访问节点, 可将非0节点到最近0节点的最短距离初始化为最大整数值,

假设当前遇到节点m[i][j], 它的相邻节点已经计算过了,最短距离为dist, 若访问过此节点, 那么此节点对应的最短距离一定满足 dis[i][j] > dist + 1 为 false.

func updateMatrix(mat [][]int) [][]int {
    dists := make([][]int, len(mat))
    for i := range dists {
        dists[i] = make([]int, len(mat[0]))
    }

    // Queue
    queue := [][]int{}
    // 初始化
    for r := range mat {
        for c := range mat[r] {
            if mat[r][c] == 0 {
                // 入队
                queue = append(queue, []int{r, c})
                // 最短距离 0
                dists[r][c] = 0
            } else { // 非0节点 
                // 初始化为最大整数 
                dists[r][c] = math.MaxInt
            }
        }
    }

    // 移动方向 上下左右
    dirs := [][]int{{-1,0}, {1, 0}, {0, -1}, {0, 1}}
    // BFS 
    for len(queue) > 0 {
        // 出队
        cur := queue[0]
        queue = queue[1:]

        dist := dists[cur[0]][cur[1]]
        // 相邻节点
        for _, dir := range dirs {
            r := cur[0] + dir[0]
            c := cur[1] + dir[1]
            // 合法坐标
            isValid := r >=0 && r < len(mat) && c >= 0 && c < len(mat[0])
            if isValid {
                // 未访问
                if dists[r][c] > dist+1 {
                    dists[r][c] = dist + 1
                    // 入队
                    queue = append(queue, []int{r, c})
                }
            }
        }
    }

    return dists
}

15.2.4 问题108: 单词演变

LCR 108. 单词接龙

在字典（单词列表） wordList 中，从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列：

• 序列中第一个单词是 beginWord 。
• 序列中最后一个单词是 endWord 。
• 每次转换只能改变一个字母。
• 转换过程中的中间单词必须是字典 wordList 中的单词。

给定两个长度相同但内容不同的单词 beginWord 和 endWord 和一个字典 wordList ，找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

提示：

• 1 <= beginWord.length <= 10
• endWord.length == beginWord.length
• 1 <= wordList.length <= 5000
• wordList[i].length == beginWord.length
• beginWord、endWord 和 wordList[i] 由小写英文字母组成
• beginWord != endWord
• wordList 中的所有字符串 互不相同

15.2.4.1 分析&题解

// TODO: 2023-09-17

15.2.5 问题109: 开密码锁

LCR 109. 打开转盘锁

一个密码锁由 4 个环形拨轮组成，每个拨轮都有 10 个数字： '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转：例如把 '9' 变为 '0'，'0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 '0000' ，一个代表四个拨轮的数字的字符串。

列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

字符串 target 代表可以解锁的数字，请给出解锁需要的最小旋转次数，如果无论如何不能解锁，返回 -1 。

示例 1:

输入：deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出：6
解释：
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的，因为当拨动到 "0102" 时这个锁就会被锁定。

示例 2:

输入: deadends = ["8888"], target = "0009"
输出：1
解释：
把最后一位反向旋转一次即可 "0000" -> "0009"。

示例 3:

输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出：-1
解释：
无法旋转到目标数字且不被锁定。

示例 4:

输入: deadends = ["0000"], target = "8888"
输出：-1

提示：

• 1 <= deadends.length <= 500
• deadends[i].length == 4
• target.length == 4
• target 不在 deadends 之中
• target 和 deadends[i] 仅由若干位数字组成

15.2.5.1 分析&题解

如果问题是关于某个事物状态的改变, 可以考虑将其转换为图的搜索问题. 事物的每种状态可以用节点标识, 若一个状态能够转换成另一个状态, 那么节点之间有边相连.

因为广度优先搜索是按照最短路径进行搜索, 所以最短路径问题可以使用广度优先. 因为要最短路径的长度, 那么需要使用双队列:

1. 当前层节点存入q1

2. q1节点出队, 将其相邻节点加入到队列 q2 . 重复2) 直到q1为空

3. 将q1, q2交换(切换当前操作的队列); 路径距离加一; 重复2)

4. 两个队列均为空, 搜索结束

由于密码包含锁定状态, 遇到时需要结束搜索.

func openLock(deadends []string, target string) int {
    init := "0000" // 初始

    // 锁定 哈希表
    mDead := make(map[string]bool) 
    for _, d := range deadends {
        mDead[d] = true
    }

    // 边界
    if mDead[init] || mDead[target] {
        return -1
    }

    // 已访问状态 哈希表
    mVisited := make(map[string]bool) 
    
    // 双队列
    queue1 := []string{init}
    queue2 := []string{}

    steps := 0 // 路径长
    // BFS
    for len(queue1) > 0 {
        // 出队
        cur := queue1[0]
        queue1 = queue1[1:]
        // 解锁
        if cur == target {
            return steps
        }

        // 相邻节点入队
        adjs := getAdjs(cur)
        for _, adj := range adjs {
            // 不是锁定码 且 未访问
            if !mDead[adj] && !mVisited[adj] {
                queue2 = append(queue2, adj)
                mVisited[adj] = true
            } 
        }

        // 下一层
        if len(queue1) == 0 {
            queue1 = queue2 
            queue2 = []string{}
            steps++
        }
    }

    return -1
}

func getAdjs(s string) []string {
    // 共有 8 种新状态
    adjs := make([]string, 0, 8)
    
    for i, c := range s {
        var sb strings.Builder
        sb.Grow(4)

        var ch rune
        // 增加
        if c == '9' {
            ch = '0'
        } else {
            ch = c + 1
        }
        addAdjs(&sb, &adjs, s, ch, i)

        // 减少
        if c == '0' {
            ch = '9'
        } else {
            ch = c - 1
        }
        addAdjs(&sb, &adjs, s, ch, i)
    }

    return adjs
}

func addAdjs(sb *strings.Builder, adjs *[]string, s string, ch rune, i int) {
        sb.WriteString(s[:i])
        sb.WriteRune(ch)
        sb.WriteString(s[i+1:])
        *adjs = append(*adjs, sb.String())
        // Reset builder
        sb.Reset()
}

15.2.6 问题110: 所有路径

LCR 110. 所有可能的路径

给定一个有 n 个节点的有向无环图，用二维数组 graph 表示，请找到所有从 0 到 n-1 的路径并输出（不要求按顺序）。

graph 的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些结点（译者注：有向图是有方向的，即规定了 a→b 你就不能从 b→a ），若为空，就是没有下一个节点了。

示例 1：

img

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

img

输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

示例 3：

输入：graph = [[1],[]]
输出：[[0,1]]

示例 4：

输入：graph = [[1,2,3],[2],[3],[]]
输出：[[0,1,2,3],[0,2,3],[0,3]]

示例 5：

输入：graph = [[1,3],[2],[3],[]]
输出：[[0,1,2,3],[0,3]]

提示：

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i
• 保证输入为有向无环图 (GAD)

15.2.6.1 分析&题解

得出所有路径, 使用深度优先搜索, 实际上使用的是回溯法.

若是无向图, 注意记录访问情况, 避免重复访问; 有向且无环图无需记录

func allPathsSourceTarget(graph [][]int) [][]int {
    res := [][]int{}
    path := []int{}
    var dfs func(int)
    dfs = func(src int) {
        // 添加到路径
        path = append(path, src)
        // 到达最后节点
        if src == len(graph)-1 {
            tmp := make([]int, len(path))
            copy(tmp, path)
            res = append(res, tmp)
        } else {
            // 搜索
            for _, n := range graph[src] {
                dfs(n)
            }
        }
        // 回溯
        path = path[:len(path)-1]
    }
    dfs(0)

    return res
}

15.2.7 问题111: 计算除法

LCR 111. 除法求值

给定一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

**注意：**输入总是有效的。可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

示例 1：

输入：equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]

示例 2：

输入：equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出：[3.75000,0.40000,5.00000,0.20000]

示例 3：

输入：equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出：[0.50000,2.00000,-1.00000,-1.00000]

提示：

• 1 <= equations.length <= 20
• equations[i].length == 2
• 1 <= Ai.length, Bi.length <= 5
• values.length == equations.length
• 0.0 < values[i] <= 20.0
• 1 <= queries.length <= 20
• queries[i].length == 2
• 1 <= Cj.length, Dj.length <= 5
• Ai, Bi, Cj, Dj 由小写英文字母与数字组成

15.2.7.1 分析&题解

图可以用于标识物体和物体间的关系, 节点表示物体, 物体之间的关系用变量表示. 在此问题中, 节点表示变量, 变量直接的关系为除法, 商为边的权重; 又因为 a/b和b/a一般不同, 所以可以构建一个有向的含环的带权重的图.

以equations = [["a","b"],["b","c"]], values = [2.0,3.0] 为例:

image-20230917220856897

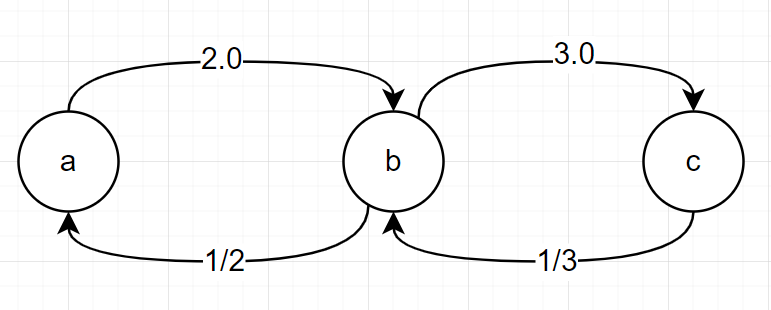
因为含有环, 所以需要标记节点是否被访问过了.

计算变量之间的商, 实际上是找出从节点A到节点B的路径, 那么A/B的结果就是边权重的乘积.

例如: c/a 表示从节点c出发到a, 结果为$\frac{1}{3}\times \frac{1}{2} = \frac{1}{6}$

使用map[string]map[string]float64构建邻接表, 深度优先遍历寻找结果.

func calcEquation(equations [][]string, values []float64, queries [][]string) []float64 {
    // 邻接表
    graph := buildGraph(equations, values)
    
    res := make([]float64, len(queries))
    // 求解
    for i := range queries {
        from := queries[i][0]
        to := queries[i][1]
        
        _, fromOk := graph[from]
        _, toOk := graph[to]
        if !fromOk || !toOk {// 不在图中, 无解
            res[i] = -1
        } else {
            // 访问标识
            visited := make(map[string]bool) 
            res[i] = dfs(graph, visited, from, to)
        }
    }

    return res
}

func dfs(graph map[string]map[string]float64, visited map[string]bool, from, to string) float64 {
    if from == to {
        return 1
    }

    visited[from] = true
    for next, val := range graph[from] {
        // 未访问
        if !visited[next] {
            nextVal := dfs(graph, visited, next, to)
            if nextVal > 0 { // 有结果
                return val * nextVal
            }
        }
    }
    // 回溯, 还原状态
    visited[from] = false
    // 此路径 无解
    return -1
}

func buildGraph(eqs [][]string, vals []float64) map[string]map[string]float64 {
    graph := make(map[string]map[string]float64)

    // len(eqs) == len(vals)
    for i := 0; i < len(vals); i++ {
        var1, var2 := eqs[i][0], eqs[i][1]
        val := vals[i]
        
        // var1 / var2 
        if _, ok := graph[var1]; !ok {
            m := make(map[string]float64)
            graph[var1] = m
        }
        graph[var1][var2] = val 

        // var2 / var1
        if _, ok := graph[var2]; !ok {
            m := make(map[string]float64)
            graph[var2] = m
        } 
        graph[var2][var1] = 1 / val
    }

    return graph
}

15.2.8 问题112: 最长递增路径

LCR 112. 矩阵中的最长递增路径

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

img

输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

img

输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 2^31 - 1

15.2.8.1 分析&题解

// TODO: 2023-09-17

Reference

1. 剑指Offer（专项突破版）