15.3 拓扑排序
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.
For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks.
拓扑排序是指对一个有向无环图的节点进行排序之后得到的序列.
若存在一条从A到B的边, 那么在拓扑排序中A一定在B的前面.
一个有向无环图有一个或多个拓扑排序序列, 无向图或有向有环图不存在拓扑排序序列.
15.3.1 Kahn's algorithm
入度: 节点v的入度是以v为终点的边的数目.
出度: 节点v的出度是以v为起点的边的数目.
流程:
- 取出一个入度为0的节点, 放入拓扑排序序列;
- 删除该节点以及所有以它为起点的边; 继续步骤 1) 直到图为空或不存在入度为0的节点.
若图为空则找到了拓扑排序序列.
若图不为空并且不存在入度为0的节点, 那么图一定有环.
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
while S is not empty do
remove a node n from S
add n to L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
此算法可以寻找拓扑排序或者判断是否有环.
15.3.2 问题113: 课程排序
现在总共有
numCourses门课需要选,记为0到numCourses-1。给定一个数组
prerequisites,它的每一个元素prerequisites[i]表示两门课程之间的先修顺序。 例如prerequisites[i] = [ai, bi]表示想要学习课程ai,需要先完成课程bi。请根据给出的总课程数
numCourses和表示先修顺序的prerequisites得出一个可行的修课序列。可能会有多个正确的顺序,只要任意返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
示例 1:
输入: numCourses = 2, prerequisites = [[1,0]] 输出: [0,1] 解释: 总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。示例 2:
输入: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]] 输出: [0,1,2,3] or [0,2,1,3] 解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。 因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。示例 3:
输入: numCourses = 1, prerequisites = [] 输出: [0] 解释: 总共 1 门课,直接修第一门课就可。提示:
1 <= numCourses <= 20000 <= prerequisites.length <= numCourses * (numCourses - 1)prerequisites[i].length == 20 <= ai, bi < numCoursesai != biprerequisites中不存在重复元素
15.3.2.1 分析&题解
将课程当作节点, 课程先后顺序左右边, 构建有向图.
例如: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
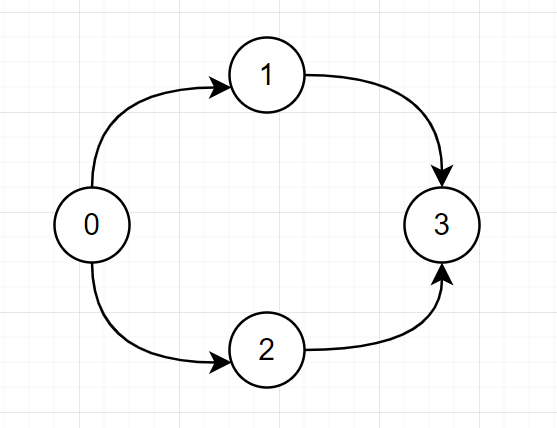
课程的顺序实际就是图的拓扑排序序列, 问题就变成了求有向图的拓扑排序序列.
func findOrder(numCourses int, prerequisites [][]int) []int {
// 构建有向图
graph := make(map[int][]int, numCourses)
for i := 0; i < numCourses; i++ {
s := make([]int, 0)
graph[i] = s
}
// 邻接表
inDegrees := make([]int, numCourses) // 节点入度
for _, pre := range prerequisites {
graph[pre[1]] = append(graph[pre[1]], pre[0])
inDegrees[pre[0]]++
}
// 广度优先搜索入度为0的节点
queue := make([]int, 0)
for i, d := range inDegrees {
if d == 0 {
queue = append(queue, i)
}
}
// 拓扑排序序列
res := make([]int, 0, numCourses)
for len(queue) > 0 {
cur := queue[0]
queue = queue[1:]
// 加入拓扑排序序列
res = append(res, cur)
// 删除以 cur 为起点的边
for _, adj := range graph[cur] {
inDegrees[adj]--
// 添加新的入度为 0 的节点
if inDegrees[adj] == 0 {
queue = append(queue, adj)
}
}
}
if len(res) == numCourses {
return res
}
return []int{}
}
15.3.3 问题114: 外星文字典
现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。
给定一个字符串列表
words,作为这门语言的词典,words中的字符串已经 按这门新语言的字母顺序进行了排序 。请你根据该词典还原出此语言中已知的字母顺序,并 按字母递增顺序 排列。若不存在合法字母顺序,返回
""。若存在多种可能的合法字母顺序,返回其中 任意一种 顺序即可。字符串
s字典顺序小于 字符串t有两种情况:
- 在第一个不同字母处,如果
s中的字母在这门外星语言的字母顺序中位于t中字母之前,那么s的字典顺序小于t。- 如果前面
min(s.length, t.length)字母都相同,那么s.length < t.length时,s的字典顺序也小于t。示例 1:
输入:words = ["wrt","wrf","er","ett","rftt"] 输出:"wertf"示例 2:
输入:words = ["z","x"] 输出:"zx"示例 3:
输入:words = ["z","x","z"] 输出:"" 解释:不存在合法字母顺序,因此返回 "" 。提示:
1 <= words.length <= 1001 <= words[i].length <= 100words[i]仅由小写英文字母组成
15.3.3.1 分析&题解
// TODO: 2023-09-18
15.3.4 问题115: 重建序列
给定一个长度为
n的整数数组nums,其中nums是范围为[1,n]的整数的排列。还提供了一个 2D 整数数组sequences,其中sequences[i]是nums的子序列。 检查nums是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列,并且所有序列sequences[i]都是它的子序列。对于给定的数组sequences,可能存在多个有效的 超序列 。
- 例如,对于
sequences = [[1,2],[1,3]],有两个最短的 超序列 ,[1,2,3]和[1,3,2]。- 而对于
sequences = [[1,2],[1,3],[1,2,3]],唯一可能的最短 超序列 是[1,2,3]。[1,2,3,4]是可能的超序列,但不是最短的。如果
nums是序列的唯一最短 超序列 ,则返回true,否则返回false。子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素,而不改变其余元素的顺序的序列。示例 1:
输入:nums = [1,2,3], sequences = [[1,2],[1,3]] 输出:false 解释:有两种可能的超序列:[1,2,3]和[1,3,2]。 序列 [1,2] 是[1,2,3]和[1,3,2]的子序列。 序列 [1,3] 是[1,2,3]和[1,3,2]的子序列。 因为 nums 不是唯一最短的超序列,所以返回false。示例 2:
输入:nums = [1,2,3], sequences = [[1,2]] 输出:false 解释:最短可能的超序列为 [1,2]。 序列 [1,2] 是它的子序列:[1,2]。 因为 nums 不是最短的超序列,所以返回false。示例 3:
输入:nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]] 输出:true 解释:最短可能的超序列为[1,2,3]。 序列 [1,2] 是它的一个子序列:[1,2,3]。 序列 [1,3] 是它的一个子序列:[1,2,3]。 序列 [2,3] 是它的一个子序列:[1,2,3]。 因为 nums 是唯一最短的超序列,所以返回true。提示:
n == nums.length1 <= n <= 104nums是[1, n]范围内所有整数的排列1 <= sequences.length <= 10^41 <= sequences[i].length <= 10^41 <= sum(sequences[i].length) <= 10^51 <= sequences[i][j] <= nsequences的所有数组都是 唯一 的sequences[i]是nums的一个子序列
15.3.4.1 分析&题解
超序列和子序列是两个相对的概念.若序列A中的所有元素按照先后顺序在B中出现, 那么A是B的子序列, B是A的超序列.
将seqs中的所有数字看成节点, 相邻的数字有一条前面数字指向后面的边, 构成一个有向图.
以nums = [1,2,3], sequences = [[1,2],[1,3]] 为例:
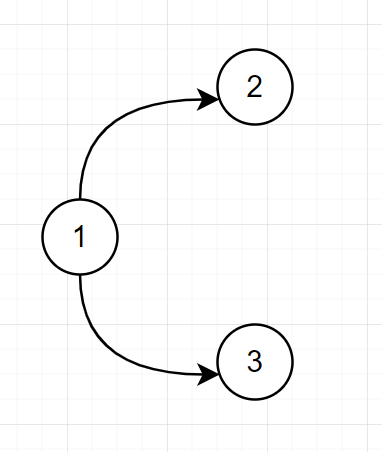
由seqs重建的序列为图的拓扑排序序列, 那么问题就变成了, 拓扑排序序列是否唯一并且为 nums.
func sequenceReconstruction(nums []int, sequences [][]int) bool {
// 构建有向图
inDegrees := make(map[int]int, len(nums)) // 入度
graph := make(map[int][]int, len(nums))
for _, seq := range sequences {
if len(seq) <= 1 {
if _, ok := graph[seq[0]]; !ok {
s := make([]int, 0)
graph[seq[0]] = s
}
if _, ok := inDegrees[seq[0]]; !ok {
inDegrees[seq[0]] = 0
}
}
for i := 0; i < len(seq)-1; i++ {
if _, ok := graph[seq[i]]; !ok {
s := make([]int, 0)
graph[seq[i]] = s
}
graph[seq[i]] = append(graph[seq[i]], seq[i+1])
// 入度增加
if _, ok := inDegrees[seq[i]]; !ok {
inDegrees[seq[i]] = 0
}
inDegrees[seq[i+1]]++
}
}
// 入度为0的节点
queue := make([]int, 0)
for k, v := range inDegrees {
if v == 0 {
queue = append(queue, k)
}
}
// 拓扑排序序列
res := make([]int, 0, len(nums))
// 寻找唯一拓扑排序序列
for len(queue) == 1 {
cur := queue[0]
queue = queue[1:]
// 添加至拓扑序列
res = append(res, cur)
// 删除边
for _, adj := range graph[cur] {
inDegrees[adj]--
if v, ok := inDegrees[adj]; ok && v == 0 {
queue = append(queue, adj)
}
}
}
return reflect.DeepEqual(res, nums)
}
